Recent advancements in quantum technologies shed light on viable quantum computation in the near future. Quantum circuit simulation plays a vital role in the toolchain of quantum hardware and software development. Particularly, quantum program compilation and verification require efficient simulation engines. However, due to the enormous Hilbert space of quantum states, simulating quantum circuits on classical computers is notoriously challenging yet indispensable for quantum system construction, especially in the noisy intermediate-scale quantum (NISQ) era. Even with powerful quantum computers, simulating quantum circuits on classical computers will remain helpful due to its strong simulation ability to obtain complete quantum state information in contrast to sampling-based profiling of quantum systems, which are intrinsically probabilistic. Given the importance of classical simulation of quantum circuits, our recent work advances the state of the art in two dimensions: accuracy (by representing complex numbers algebraically in integers) and scalability (by bit-slicing integer representation and achieving matrix-vector multiplication with symbolic Boolean manipulation). Thereby, we developed a new quantum circuit simulator named SliQSim. Experimental results demonstrate the superiority of our method to prior state-of-the-art tools over various quantum circuits. For certain quantum circuit families, SliQSim can simulate instances with up to tens of thousands of qubits. With its distinct accuracy and outstanding scalability, we envisage the broad application of SliQSim on quantum circuit compilation and verification tasks.

Quantum computation is a new computation paradigm based on quantum mechanics, whose non-classical properties, such as superposition and entanglement, offer extraordinary resources to achieve computation and information processing power beyond the reach of classical computers. Theoretical demonstrations of the superiority of quantum algorithms, e.g., in number factorization, quantum system simulation, database search, counting, machine learning, optimization, etc., have motivated physicists and engineers to build ever more powerful quantum computers. On the hardware side, different implementation methods based on ion traps, nuclear magnetic resonance, photonics, solid-state, superconductors, and so on are under active research. On the software side, new programming languages, compilers, and application tools have to be developed. New tools are much needed to release the true power of quantum computers. 

The hardware design and software compilation of quantum computation are closely related to electronic design automation (EDA). Particularly, program compilation for quantum computers requires transformations of high-level programming languages into low-level quantum assembly code, which consists of a sequence of unitary operations represented as quantum circuits. The compilation requires high-level and logic syntheses of design automation techniques. Moreover, formal verification, simulation, and emulation are essential because quantum computers are intrinsically probabilistic and noisy. A workflow of quantum program compilation is shown in the Figure 1 below. In this work, we develop an accurate and scalable quantum circuit simulator using EDA techniques.

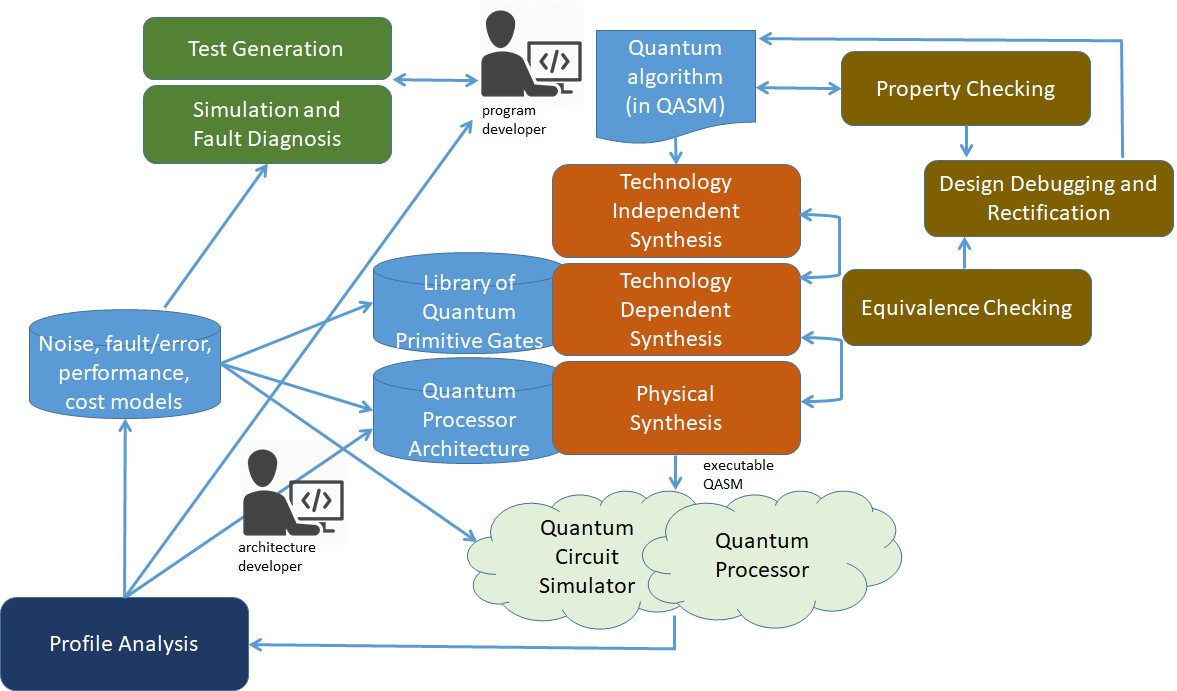
Figure 1. A workflow of quantum program compilation

Simulating quantum circuits on a classical computer is indispensable to understanding system behavior and verifying design correctness. However, the simulation is challenging because quantum states have to be described in the complex vector space, and the space is exponential in the number of quantum bits (qubits). Although there are special classes of quantum circuits, such as the stabilizer circuits, that allow efficient simulation by classical computers, simulating general quantum circuits is computationally hard. Despite the aforementioned challenges, various simulation algorithms based on different underlying data structures have been proposed and tools are available, e.g., array-based, stabilizer-specific, tensor network, and decision diagram (DD) based methods. However, these methods suffer from different issues: array-based methods represent quantum states and operators by arrays in exponential sizes, and are hardly scalable to 50 qubits even with supercomputing; stabilizer-specific methods are not general; tensor network based methods target low-depth or intermediate-size circuits, and usually exploit multi-core computing. On the other hand, although decision diagrams are well-known for their typical memory explosion problems, when engineered properly the DD-based methods can be superior to the others. The simulation method proposed in this work is DD-based. While prior DD-based methods require specializing multi-terminal or multi-valued DDs for general quantum circuit simulation, ours relies on standard binary decision diagrams (BDDs). 

The state-of-the-art method is based on the Quantum Multiple-valued Decision Diagrams (QMDDs). The data structure consists of decision nodes with multi-valued branching for matrix representation and edges weighted with complex numbers for unitary operator and state vector representation and manipulation. In contrast, we rely on BDD to represent and evolve quantum states. Moreover, unlike prior work with precision loss representing complex numbers, our method employs the algebraic representation for an accurate representation of a complex number \(α=\frac{1}{\sqrt{2}^k}（aω^3+bω^2+cω+d）\), with integers a,b,c,d and \(ω=e^\frac{iπ}{4}\), under the considered set of unitary operators general enough to achieve universal quantum computation. To the best of our knowledge, our method is the first work that utilizes the accurate representation for quantum circuit simulation. Besides the accuracy enhancement, to extend the capacity of quantum circuit simulation, we devise 1) a bit-slicing technique that represents a (\(2^n×1\)) integer vector bit by bit, for each bit corresponding to an \(n\)-variable BDD, as shown in the Figure 2 below, where an integer is encoded in r bits, and 2) an implicit method that replaces matrix-vector multiplication with a set of pre-characterized Boolean formulas of the unitary operators for BDD manipulation.

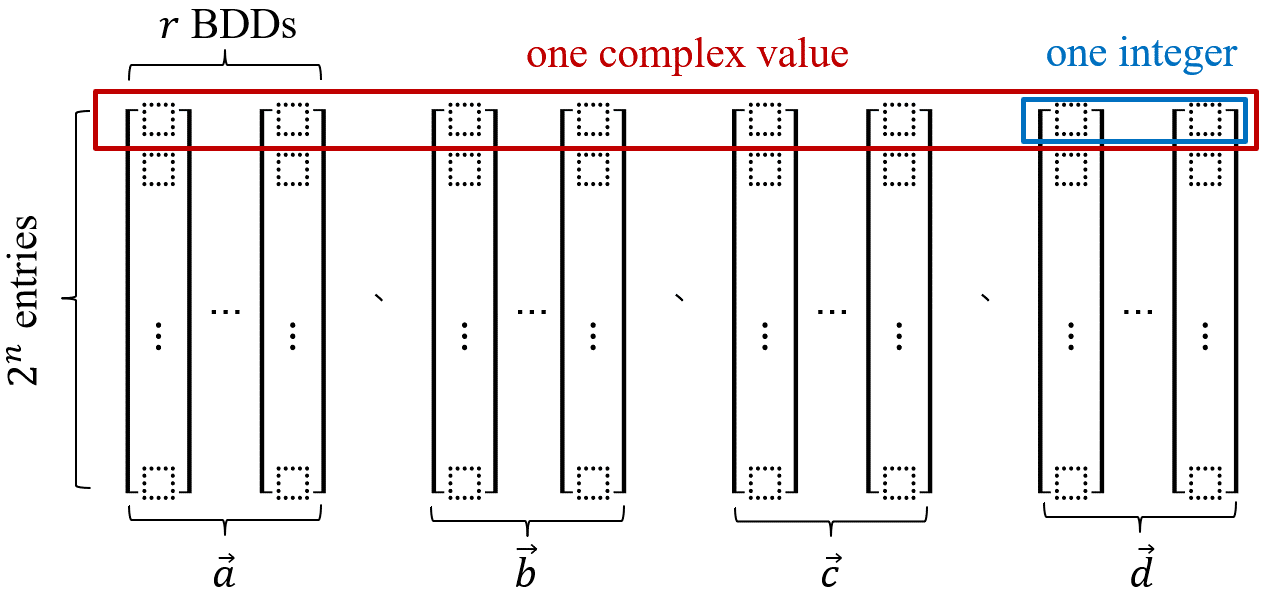
Figure 2. A bit-slicing technique
 

The proposed methods were implemented in the C++ language, and the simulator named SliQSim (available at https://github.com/NTU-ALComLab/SliQSim) was developed. Experimental results demonstrate the accuracy and scalability advantages of SliQSim compared to the state-of-the-art over a number of different benchmarks. Notably, for certain benchmark families, our method can simulate circuits up to tens of thousands of qubits beyond the capacity of other existing simulators. The detailed experimental results can be found in the reference below. For future work, we plan to extend our methods to quantum circuit equivalence checking, which is crucial to the quantum system design flow in order to check the equivalence between two circuits at the same or different abstraction levels. Also, we seek potential applications of SliQSim, e.g., quantum volume calculation, etc. 

Reference: Yuan-Hung Tsai, Jie-Hong Roland Jiang, and Chiao-Shan Jhang. Bit-Slicing the Hilbert Space: Scaling Up Accurate Quantum Circuit Simulation. In Proceedings of the 58th ACM/IEEE Design Automation Conference (DAC), pp. 439-444, 2021.