量子技術的快速進展預示量子計算時代的來臨。量子電路模擬在量子硬體與軟體的工具鏈扮演要角，尤其對於量子程式的編譯與驗證。因量子態有巨大的希爾伯特空間，在古典電腦上模擬量子電路具高度挑戰，然而有別於概率性的基於抽樣的量子系統分析，古典電腦強模擬可以獲得完整的量子狀態資訊，因而對於建構量子系統卻不可或缺，尤其在現今有雜訊的中等規模量子（Noisy Intermediate Scale Quantum，NISQ）時代。鑑於量子電路模擬的重要性，研究團隊在兩個層面上推進了量子電路模擬的技術界線：準確性（藉由代數方法表示複數）和可擴展性（藉由對整數進行位切片並使用布林算式實現矩陣向量乘法），並開發新量子電路模擬器SliQSim。實驗結果證明新量子電路模擬器SliQSim的優越性，對於特定系列的量子電路，其可以模擬多達數萬個量子位元的電路。未來在量子電路編譯和驗證上將有廣泛的應用。

　　量子計算是一種基於量子力學的新型計算模型，其疊加和糾纏等非古典特性，為實現古典電腦無法企及的計算和資訊處理能力提供前所未有的工具。量子演算法在特定計算問題的處理上遠優於古典演算法，例如數值分解、量子系統模擬、數據庫搜索、計數、機器學習、組合最優化等，已激勵科學家和工程師構建功能強大的量子電腦。在硬體方面，基於離子阱、核磁共振、光子學、固態、超導體等，不同的實踐方式正在積極研究中。在軟體方面，必須開發新的程式語言、編譯器和應用工具，有了軟體工具的協助才能讓量子電腦的運算能力獲得充分的發揮。

　　量子計算的硬體設計和軟體編譯與電子設計自動化（Electronic design automation，EDA）有密切相關。特別是，量子電腦的程式編譯需要將高階語言程式轉為低階量子組合語言程式，亦即一系列基礎的么正運算所組成的抽象量子電路。編譯需要設計自動化技術裡高階與邏輯合成。此外，形式驗證、模擬和仿真是必不可少的，因為量子電腦本質上是概率性和有雜訊的。量子程式編譯的工作流程如下圖一所示。在這項工作中，研究團隊使用 EDA 技術開發了一個準確且有擴展性的量子電路模擬器。

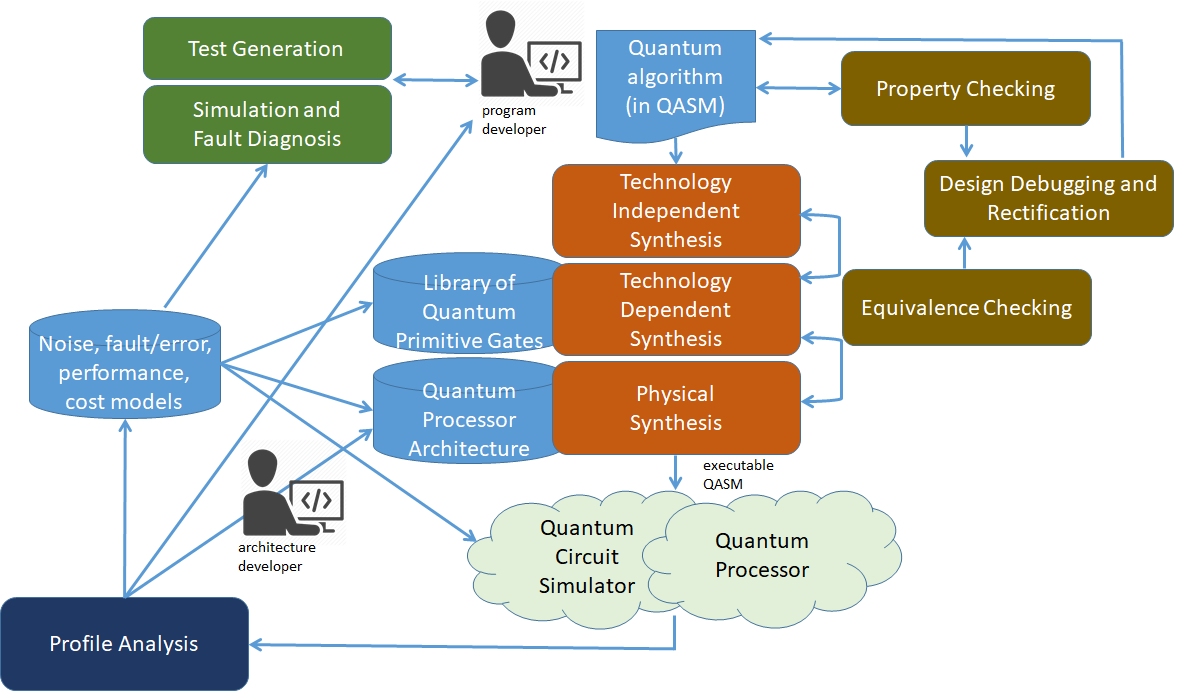
圖一：量子程式編譯的工作流程

　　在古典電腦上模擬量子電路對於理解程式行為和驗證設計正確性不可或缺。然而，必須在複數空間中描述量子態，且該空間是量子位（qubits）數量的指數倍，模擬極具挑戰性。雖然有特殊類型的量子電路，例如穩定器電路，可以通過古典電腦做有效率的模擬，但模擬泛用的量子電路在計算上極為困難。儘管存在上述挑戰，基於不同底層資料結構的各種模擬算法已被提出，例如，基於陣列、穩定器限定、張量網路和基於決策圖（Decision Diagram）的方法。然而，這些方法存在不同的問題：基於陣列的方法以指數成長的陣列表示量子態和運算子，即使利用超級電腦也很難擴展到50個量子位元；穩定器限定方法並不通用；基於張量網路的方法主要針對低深度或中等規模電路的模擬，且通常利用多核計算。

　　另一方面，雖然決策圖常有存儲空間爆增問題，但如果設計得當，基於決策圖的方法可以優於其他方法。過去基於決策圖的方法需要專門設計多端點或多數值決策分支來進行通用量子電路模擬，基於量子多數值決策圖（Quantum Multiple-valued Decision Diagrams，QMDD）具有多數值分支的決策節點及用複數加權的邊來表示矩陣，用於表示與操作么正運算子和狀態向量。而本文所提出的模擬方法與過去利用會造成準度失真的複數表示法不同，主要是基於標準的二元決策圖（Binary Decision Diagrams，BDD），以BDD來表示與更新量子態。而且，採用代數方法來精確表示一複數 \(α=\frac{1}{\sqrt{2}^k}（aω^3+bω^2+cω+d）\)，其中a,b,c,d為整數係數而\(ω=e^\frac{iπ}{4}\)，所支援的么正運算子足以實現通用的量子計算。研究團隊是首次以代數表示法來實作精確量子電路模擬的團隊。除了提高準度之外，為了擴展量子電路模擬的能力，研究團隊也提出（1）位元切片技術，以表示一個（\(2^n×1\)）維度的狀態向量，每一個位元都對應一個\(n\)變數的BDD，如下圖二所示；（2） 隱式表示方法，以預先推導一組代表么正運算子的布林公式，用BDD的操作取代矩陣向量乘法。

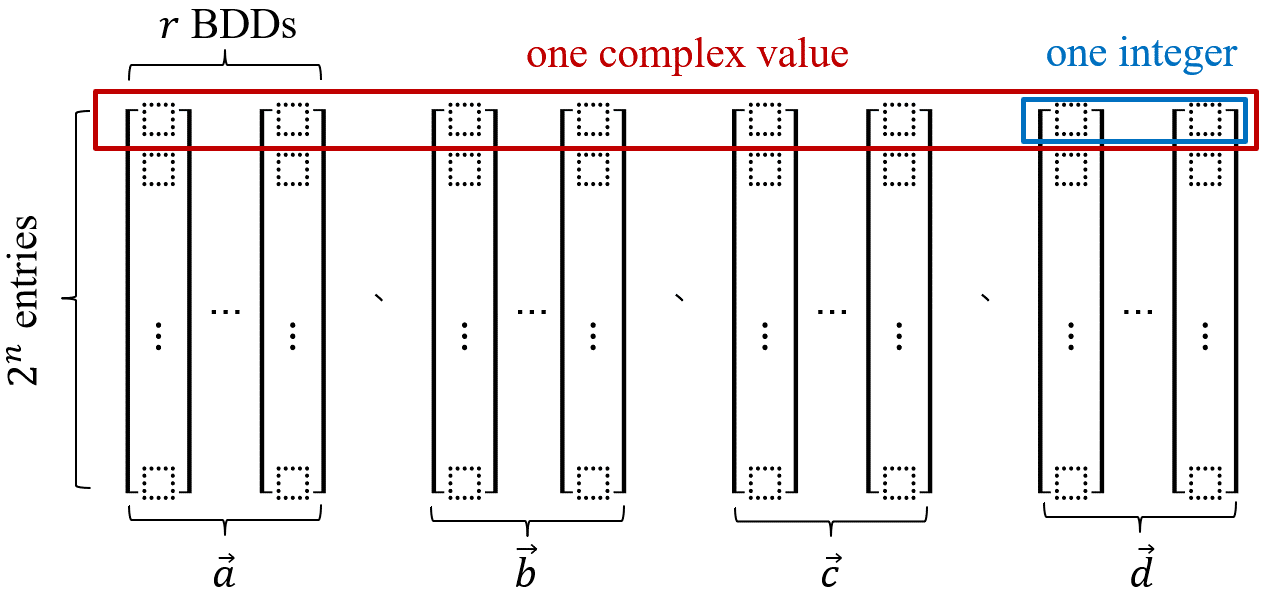
圖二：位元切片技術
 

　　本文以 C++ 語言實作名為SliQSim模擬器（開源於 https://github.com/NTU-ALComLab/SliQSim），而實驗結果證明SliQSim模擬器在許多不同基準上，與最新技術相比具有準確性和可擴展性的優勢。對於某些類型的電路，研究團隊更發現本文的研究可以模擬高達數萬個量子位的電路，超出了其他現有模擬器的能力。詳細實驗結果請參見參考文獻。研究團隊未來計劃將此方法延伸到量子電路等同驗證，這在量子系統設計流程至關重要，用以檢查不同抽象級別的兩個電路之間的等同性。此外，研究團隊也會探索SliQSim的各式應用，例如量子體積（Quantum Volume）計算等。

參考文獻：Yuan-Hung Tsai, Jie-Hong Roland Jiang, and Chiao-Shan Jhang. Bit-Slicing the Hilbert Space: Scaling Up Accurate Quantum Circuit Simulation. In Proceedings of the 58th ACM/IEEE Design Automation Conference (DAC), pp. 439-444, 2021.