We introduce our recent studies on predicting the winning price in a real time bidding auction of online advertisements. Previous studies mainly solve the problem from the view of sellers, while we focus on the view of buyers. A major challenge is that the buyer does not always possess the complete information about the winning price, especially for those losing bids in the past. We present how we solve this problem by proposing a unified framework that models both the observed and unobserved data simultaneously through analytics on historical bidding log. The framework offers flexibility for different combinations of deep learning structures and the different distribution of winning prices.

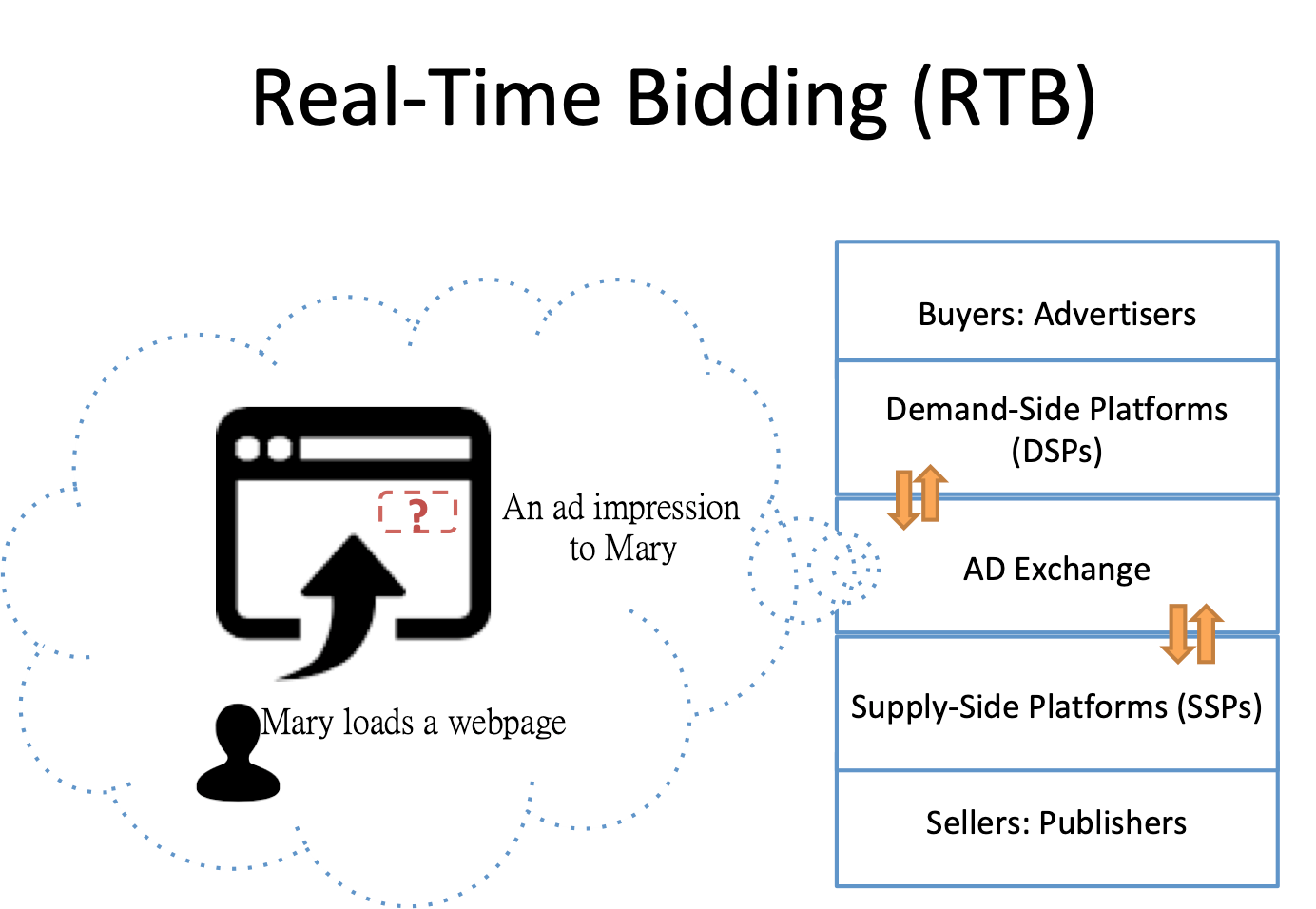
Real-Time Bidding (RTB) is a programmatic method that allows advertisers and publishers to trade each ad independently in online advertising. More specifically, RTB is a mechanism to trade the “opportunity” to display an ad to a user browsing a webpage; this opportunity is called an “impression.” Since one webpage can be browsed by different users, a huge number of impressions could be traded every second. It is thus inevitable for both the publishers and advertisers to rely on software to buy and sell these impressions automatically on a massive scale. As a result, there are agents of advertisers, which are called the Demand-Side Platform (DSP), and agents of suppliers, which are called the Supply-Side Platform (SSP), to help with this programmatic trading. The system hosting the trading is called the ad exchange system.  

A rough trading process of an ad impression can be as follows. Suppose Mary is browsing a webpage and the supplier starts to sell the impression. With the help of the SSP, the supplier passes the information of the impression to the ad exchange system and starts an auction immediately. Many DSPs will receive the auction event, and some of them will bid on the impression with different bidding prices. After receiving the bids, the ad exchange system will deliver the winner’s ad to the website. All of the above steps should be completed in less than one second, so the ad can be displayed for Mary in real time. When Mary sees the ad on her device, the ad exchange system will charge the winner’s DSP and share the money to the SSP and the supplier. The DSP can then charge the advertiser if Mary clicks the ad. 

Usually, RTB auctions use the rule of second price auction, where the DSP with the highest bid wins and pays the second-highest bid. Figure 1 offers an example. From the standpoint of a DSP in RTB, we define the “winning price” of the DSP as the price to win the auction. More specifically, it is the highest bidding price offered by its opponent. Therefore, this value is different for different DSPs. For example, four DSPs A, B, C, and D offer bids 50, 100, 150, and 200, respectively. The winning price of DSPs A, B, and C is 200, and the winning price of DSP D is 150. There are two reasons we study the winning price. First, the winning price is usually the same as the cost of winning the bid. In practice, the budget of the DSP is limited, and the cost is hence an important factor of the bidding strategy. Second, the winning price is an indicator of the importance of an impression or the importance of the audience in the market, and this importance can help the DSP estimate the value of the impression more accurately. If the DSP wants to use the winning price to help its bidding strategy design or value estimation, it needs to predict the winning price. 

However, predicting the winning price is not easy. According to the mechanism of the modern RTB, the winning price is observable only to the DSP that wins the bid. In the previous example, only the DSP D knows its winning price is 150 because the ad exchange system charges DSP D 150 after the auction. DSPs A, B, and C know only that they did not win. An important observation is that DSPs A, B, and C do know a lower bound of the winning price, which is their bidding price. For example, DSP A knows the winning price is at least 50, because otherwise it would have won. 

In our research, we study how to construct the winning price model based on the historical bidding logs. We split the data into two groups by the bidding result. One group is won data, where the winning price is observed. The other is lost data, where only the lower bound of the winning price is known. We study how to fit a model based on both won data and lost data using the linear and the censored regression models. However, neither of the two models can always outperform the other and thus we propose a mixed model, which is an ensemble of the two models weighted by the winning rate. 

Recently, researchers have proposed some deep-learning models to predict the clickthrough rate (CTR) of an impression and shown their outperformance compared to the linear model. Because the features of the winning price prediction problem are similar to those of the CTR prediction problem, we study how to use these models to predict the winning price. However, fitting the deep-learning models from the lost data is not a trivial matter. In our research, we proposed a generalized winning price model that has the flexibility to combine different deep-learning structures and the underlying winning price distributions. The new model has the ability to learn from both won data and lost data. Figure 2 offers an example of the generalized winning price model. 

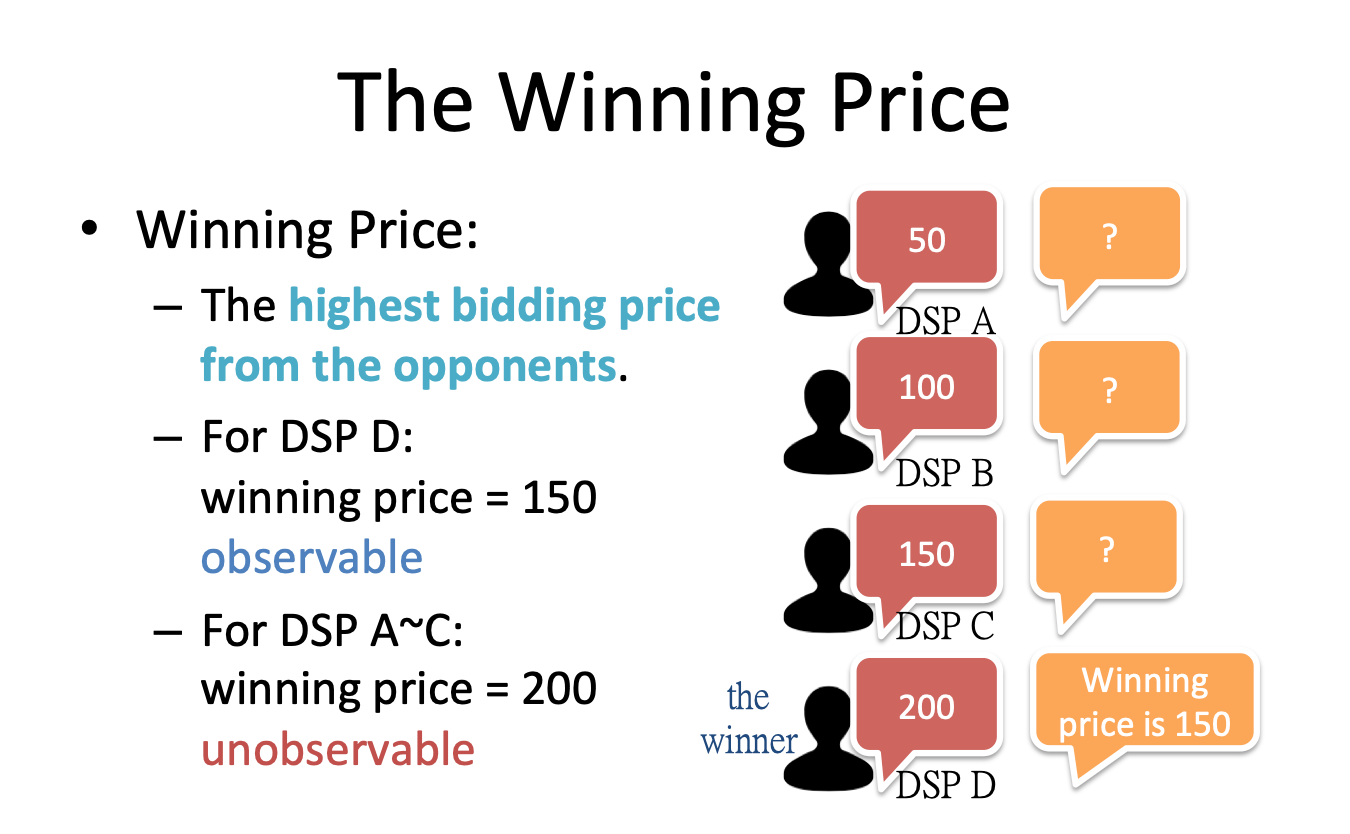
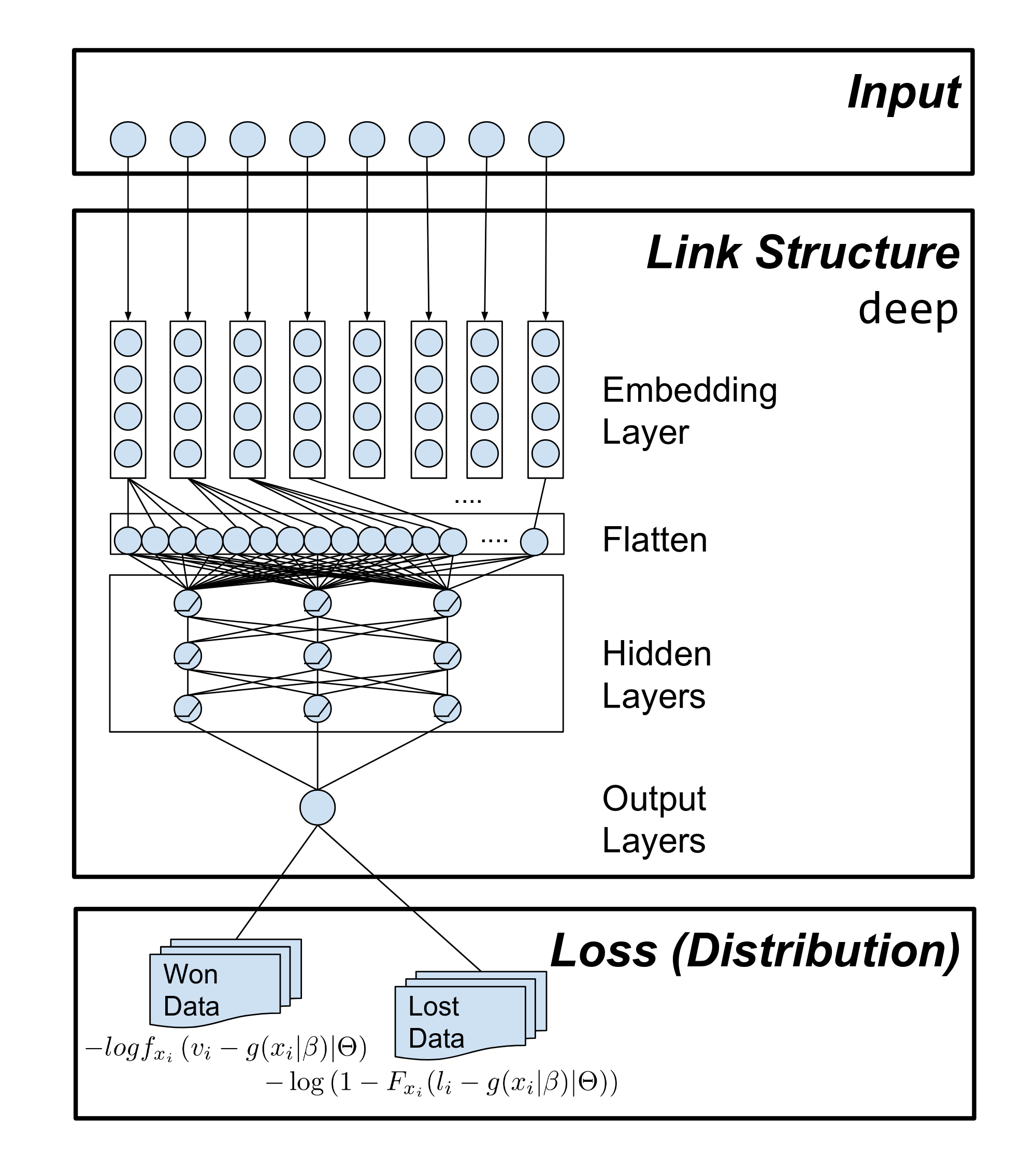
Figure 2. The proposed generalized winning price model. The link structure deep can be replaced by different structures. The loss is related to the assumption of the winning price distribution. If the cumulative density function and the probability density function of the distribution are known as F and f, then the loss of the won data and lost data are the formula in the figure.