後量子密碼學（post-quantum cryptography，PQC）是一個研究能夠抵禦量子破密的密碼學分支。在2016年，美國國家標準暨技術研究院宣布開始徵集後量子密碼系統。本研究主要探討晶格密碼系統：Dilithium、Kyber、NTRU、NTRU Prime和Saber。為兼顧效能及安全性，研究團隊用組合語言來實作當中最耗時的運算：多項式乘法和各種變換，並討論Armv7-M、Armv7E-M和Armv8-A三個主要架構。

　　快速傅立葉變換（fast Fourier transform，FFT）可用來加速多項式乘法的計算。除了最廣為人知的 Cooley-Tukey FFT，研究團隊在Cortex-M4上實作了Good-Thomas FFT和Rader FFT。後續指出了如何在NTRU和Saber上利用FFT來加速計算。在Saber上，研究團隊額外深入討論其記憶體的用量、與遮罩防護的相容性和Cortex-M3上的實作。最後，在Armv8-A的架構下提出“Barrett multiplication”和“asymmetric multiplication”來優化Dilithium、Kyber和Saber在Cortex-A72和Apple M1上的實作。

 後量子密碼學–以現代電腦抵禦量子破密

　　量子電腦蓬勃的發展勢必會威脅到生活中的隱私。後量子密碼學（post-quantum cryptography，PQC）是一個研究能夠抵禦量子破密的密碼學分支。相較於常見的對稱式密碼系統只需要兩倍長的金鑰就可有同樣的安全性，基於 RSA和ECC的公鑰密碼系統在 Shor 演算法的攻擊下將被破解。在 PQC 中，公鑰密碼系統主要歸類為以下五類：晶格密碼系統、編碼密碼系統、雜湊函式密碼系統、多變量密碼系統和超奇異橢圓曲線同源密碼系統。

NIST後量子密碼學標準化競賽

　　在 2016 年，美國國家標準暨技術研究院（National Institute of Standards and Technology，NIST）在 PQCrypto會議上宣布開始徵集後量子密碼系統。2017年11月30日截止收件時共有82組投稿。經過兩輪的篩選，2020年7月NIST 公告七組決選者和八組備選者。決選者中，有五個晶格密碼系統、一個編碼密碼系統和一個多變量密碼系統。備選者中，有兩個晶格密碼系統。晶格密碼系統顯然因為其總體性能優越而佔了絕大多數的晉級名額。決選者可能在第三輪後即成為標準，備選者則還需經過第四輪。本文主要討論以下五個晶格密碼系統的成果：Dilithium、Kyber、NTRU、NTRU Prime和Saber。並專注於這些密碼系統中最消耗時間的計算：多項式乘法和其變換。

組合語言的重要性

　　C語言是一個通用程式語言。因其精細的記憶體調控能力，資深程式設計師所寫的C程式通常被視為優化的實作。然而在密碼學實作上，C程式通常只被做為參考實作，而不論及效能和各平台的安全性。密碼學實作中，目標是寫出全世界最快的程式，記憶體配置只是其中一個影響因素。效能良好且安全的實作常常用到平台的特殊指令和組合語言。本文主要探討 Cortex-M3、Cortex-M4、Cortex-A72三個中央處理器（central processing unit，CPU）和Apple M1晶片，並使用Armv7-M、Armv7E-M、Armv8-A 三個架構的組合語言下，和當前的優化實作做比較（多項式乘法、數論變換（number-theoretic transform，簡稱NTT）、快速傅立葉變換的詳細說明請參見備註一）。

研究成果：“Polynomial Multiplication in NTRU Prime”

　　研究團隊主要專注於NTRU Prime在Cortex-M4上的實作。如前文所述，Cooley-Tukey FFT是最常用的FFT，研究團隊更是演示Good-Thomas FFT和Rader FFT在實作中的重要性。給定互質的兩數 q_0 和 q_1，Good-Thomas FFT 是藉由重排係數來把模 (x^(q_0 q_1 )-1) 的乘積轉成模(y^(q_0 )-1,z^(q_1 )-1)的乘積。給定一個質數 p，Rader FFT 則是重排來把模 (x^p-1) 的NTT刻畫成模(x^(p-1)-1)的乘積。團隊更設計特殊的計算來實現無代價的排列，並且減少了29-32%的計算時間。

研究成果：“NTT Multiplication for NTT-unfriendly Rings”

　　研究團隊接著探討NTRU和Saber在Cortex-M4和Skylake上的實作。用NTT來進行多項式乘法必須要在係數環中找到可以用的單位根。但是在這兩個系統中，並不存在這種根。演示結果發現只要選一個夠大的係數環，仍然可以用 NTT 來乘多項式。在Cortex-M4上的NTRU多項是乘法，大幅減少 3-13% 的時間。另外，研究結果也指出在Saber中，如何用NTT來進行矩陣和向量的乘法，實作的速度更是先前的 2.5 倍。

近期研究成果

　　近期探討更多關於Dilithium、Kyber和Saber的優化。“Multi-moduli NTTs for Saber on Cortex-M3 and Cortex-M4”更進一步地討論關於Saber以下的三個考量：

1. 記憶體用量。
2. 和遮罩防護（一種防範旁通道攻擊的方法）的相容性。
3. 在 Cortex-M3上能夠防範計時攻擊的實作。

　　研究團隊在上述三個方向創下新的紀錄。另一篇“Neon NTT: Faster Dilithium, Kyber, and Saber on Cortex-A72 and Apple M1”是討論在 Armv8-A 的架構下，要如何實作 Dilithium、Kyber和Saber。在該架構下，提出了新的模乘法 “Barrett multiplication”。另外，在演算法上提出“asymmetric multiplication”來改進矩陣和向量的乘法。實作的速度在Cortex-A72和Apple M1上是先前的1.7-2.1倍。由於提出的成果均為公開且開源的原始碼，我們預期這些結果和原始碼，尤其是 “Barrett multiplication”, 會被很多將來的應用場景上採用。

非晶格密碼系統的成果

　　中央研究院在非晶格密碼系統Classic McEliece、BIKE和Rainbow也有顯著的成果。可參考“Classic McEliece on the ARM Crotex-M4”、“Optimizing BIKE for the Intel Haswell and ARM Cortex-M4”和“Rainbow on Cortex-M4”。

備註一、多項式乘法、數論變換（number-theoretic transform，簡稱NTT）、快速傅立葉變換詳細說明

多項式的乘法

給定兩多項式 \(a(x)=\sum_{i=0}^{n-1} a_i x^i\) 和 \(b(x)=\sum_{i=0}^{n-1} b_i x^i\) ，他們在模 \((x^n-ψ)\) 的乘積為 $$\sum_{i=0}^{n-1} (\sum_{j=0}^i a_j b_{i-j} + ψ\sum_{j=i+1}^{n-1} a_j b_{i-j+n}) x^i 。$$ 如果直接地去計算，需要 \(n^2 + n\) 個乘法和 \(n^2-n\) 個加法。

數論變換

在係數環中，若存在一個可逆元素 ζ 使得 \(ζ^n=ψ\) 和一個 \(n\) 次單位根 \(ω\) 滿足 $${1 \over n} \sum_{j=0}^{n-1} ω^{ij} =δ_{i,0}$$ 數論變換（number-theoretic transform，簡稱NTT）是指將多項式乘積改寫成

\(a(x)b(x) mod (x^n-ζ^n)=\sum_{i=0}^{n-1} r_i(x)a(ζω^i)b(ζω^i)\)，其中 $$r_i(x)={1 \over n} \sum_{j=0}^{n-1} (ζ^{-1} ω^{-i} x)^j 。$$

快速傅立葉變換

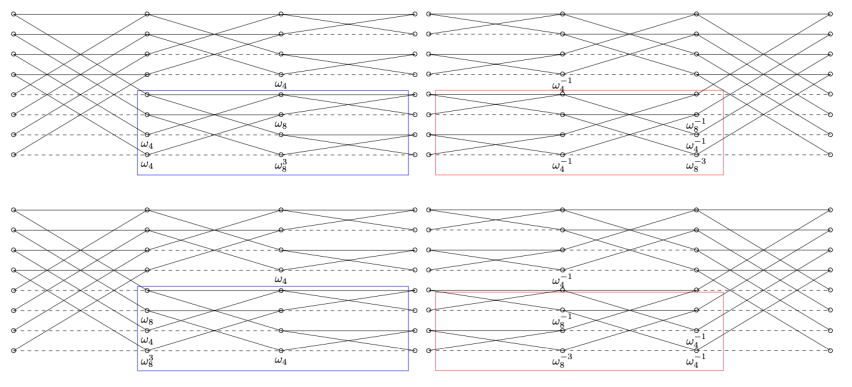
如果帶入 \(x=ζω^i\) 來計算 NTT \((a(ζ),a(ζω),…,a(ζω^{n-1}))\) ，則我們需要更多的計算。快速傅立葉變換 （fast Fourier transform，FFT）是指能夠快速計算 NTT 的方法。著名的 Cooley-Tukey FFT 是在線性時間內將

\((a(ζ),a(ζω),…,a(ζω^{n-1}))\) 的計算拆成

\((a(ζ),a(ζω^2),…,a(ζω^{n-2}))\) 和 \((a(ζω),a(ζω^3 ),…,a(ζω^{n-1}))\)。

對於 \(n=2^k\)，Cooley-Tukey FFT只需要 \({3 \over 2} n\) \(log_2 n\) + \(2n\) 個乘法和  \(3n\) \(log_2 n\) 個加減法來計算多項式乘法。