Post-quantum cryptography (PQC) is a line of research focusing on cryptosystems resisting quantum attacks. In 2016, the National Institute of Standards and Technology (NIST) announced the program Post-Quantum Cryptography Standardization. The research focused on lattice-based submissions: Dilithium, Kyber, NTRU, NTRU Prime and Saber. The team focused on the most time-consuming operations: polynomial multiplications and their transforms, and implemented assembly programs for both speed and security.

For multiplying polynomials, fast Fourier transforms (FFTs) can be used for speeding up the computations. Aside from the most commonly implemented Cooley-Tukey FFT, the team implemented Good-Thomas FFT and Rader FFT for NTRU Prime on Cortex-M4. This work was extended to how to speed up NTRU and Saber with FFTs on Cortex-M4. This work was extended with Saber in the following three directions: (i) stack usage; (ii) the compatibility with masking; and (iii) the implementation on Cortex-M3. Lastly, the team focused on Dilithium, Kyber, and Saber with Armv8-A, and proposed “Barrett multiplication” and “asymmetric multiplication” to achieve vast speedup on Cortex-A72 and Apple M1.

Post-Quantum Cryptography – Protecting Our Life From Quantum Computers with Modern Computers

The rapid development of quantum technology threatens the confidentiality of sensitive information. Post-quantum cryptography (PQC) is a line of research focusing on cryptosystems resisting quantum attacks. While doubling the key size maintains the security of symmetric-key cryptosystems, widely deployed public-key cryptosystems based on RSA and ECC are broken by Shor’s algorithm whenever large-scale quantum computers are available. In PQC, public-key cryptosystems mainly fall into the five categories: (i) lattice-based, (ii) code-based, (iii) hash-based, (iv) multivariate, and (v) supersingular elliptic curve isogeny. 

NIST’s Call for Proposals

At the conference PQCrypto 2016, the National Institute of Standards and Technology (NIST), an agency of the United States Department of Commerce, announced the program Post-Quantum Cryptography Standardization. In July 2020, NIST announced seven finalists and eight alternate candidates. Among the finalists, five are lattice-based, one is code-based, and one is multivariate. For the alternate candidates, there are two lattice-based. This article summarizes our software works on lattice-based cryptography. The research focused on the five submissions: Dilithium, Kyber, NTRU, NTRU Prime, and Saber and in particular,  on the most time-consuming operations – polynomial multiplications and their transformations.

Distinguishing Emphasis on Assembly Implementations

There is an unusual phenomenon regarding what can be called optimized implementations for practical cryptographic primitives. The C programming language is a general-purpose programming language with precise memory control. Since memory management is one of the critical factors for efficient implementations. People commonly regard nicely written C programs as fast. However, this is not the case for cryptographic implementations. The goal is to produce the fastest programs with precise control of data flows for security, and C programs are primarily for referential purposes. Optimized implementations are frequently implemented with platform-specific intrinsics and assembly instructions to reach this level of performance and guarantees. This research mainly focused on ARM assembly implementations, particularly Armv7-M, Armv7E-M, and Armv8-A for the central processing units (CPUs) Cortex-M3, Cortex-M4, Cortex-A72, and the System on Chip Apple M1. The comparisons are to optimized implementations in the literature.

Multiplication in Polynomial Rings

Multiplying polynomials \(a(x)=\sum_{i=0}^{n-1} a_i x^i\)and \(b(x)=\sum_{i=0}^{n-1} b_i x^i\) modulo \((x^n-ψ)\) is computing \(a(x)b(x)\) with the agreement \(x^n- ψ\). The result is $$\sum_{i=0}^{n-1} (\sum_{j=0}^i a_j b_{i-j} + ψ\sum_{j=i+1}^{n-1} a_j b_{i-j+n}) x^i .$$ The straightforward approach requires \(n^2 + n\) multiplications and \(n^2-n\) additions.

Number-theoretic transforms

If there is an invertible ζ in the coefficient ring satisfying \(ζ^n=ψ\) and an \(n\)-th root of unity \(ω\) satisfying $${1 \over n} \sum_{j=0}^{n-1} ω^{ij} =δ_{i,0} ,$$ number-theoretic transform (NTT), which is a ring formulation generalizing the discrete Fourier transform, characterizes the polynomial multiplication as follows:

\(a(x)b(x)  mod  (x^n-ζ^n)=\sum_{i=0}^{n-1} r_i(x)a(ζω^i)b(ζω^i)\) where $$r_i(x)={1 \over n} \sum_{j=0}^{n-1} (ζ^{-1} ω^{-i} x)^j .$$

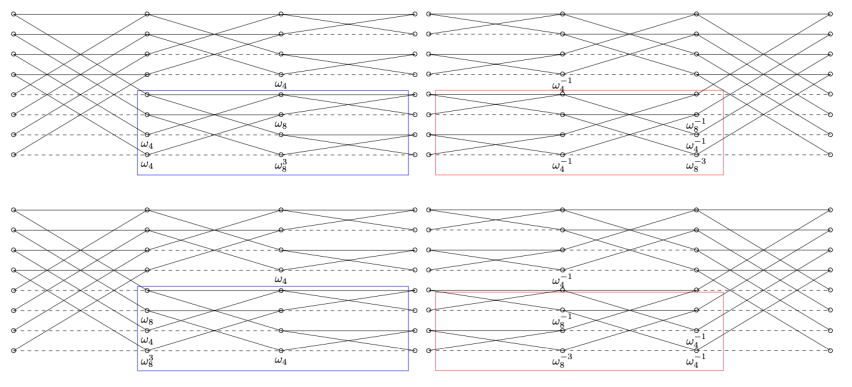
Fast Fourier Transforms

Computing the NTT \((a(ζ),a(ζω),…,a(ζω^{n-1}))\) with substitutions \(x=ζω^i\) requires even more operations. Instead, we compute all of the \(a(ζω^i)\)s simultaneously with fast Fourier transforms (FFTs). If n is even, the widely known Cooley-Tukey FFT splits the computation of

\((a(ζ),a(ζω),…,a(ζω^{n-1}))\) into
\((a(ζ),a(ζω^2),…,a(ζω^{n-2}))\) and \((a(ζω),a(ζω^3 ),…,a(ζω^{n-1}))\) in linear time.

If \(n=2^k\), applying the idea recursively computes the polynomial multiplication with only  \({3 \over 2} n\) \(log_2 n\) + \(2n\)  multiplications, and \(3n\) \(log_2 n\) additions/subtractions.

Research Contribution: Paper “Polynomial Multiplication in NTRU Prime”

This paper is a work for NTRU Prime on Cortex-M4. As mentioned previously, people commonly compute with Cooley-Tukey FFT. However, it is shown that Good-Thomas FFT and Rader FFT are also critical for implementations. For the coprime integers \(q_0\) and \(q_1\), Good-Thomas FFT transforms polynomial multiplication in \((x^{q_0 q_1}-1)\) into polynomial multiplication in \((y^{q_0}-1,z^{q_1}-1)\) by permutation. For a prime p, Rader FFT turns part of the transformation in \((x^p-1)\) into transformation in \((x^{p-1}-1)\) also by permutation. In both cases, it was achieved to be "permuted for free" by designing dedicated butterfly computations, improving the previous work by 29-32%.

Research Contribution: Paper “NTT Multiplication for NTT-unfriendly Rings”

Next, NTRU and Saber was examined on Cortex-M4 and Skylake with AVX2. NTT requires the existence of a suitable \(ω\). For both submissions, such an \(ω\) is missing in their design. It was shown that switching to a larger integer ring with a suitable \(ω\) enables NTTs. On Cortex-M4, the polynomial multiplication in NTRU was improved by 3-13%. For Saber, an overlooked optimization with NTTs was shown for the most time-consuming matrix-to-vector multiplication. The new implementation is 2.5 times faster than the previous work. 

Recent Research Works

Recently there have been several new optimizations for Dilithium, Kyber, and Saber. The new paper “Multi-moduli NTTs for Saber on Cortex-M3 and Cortex-M4” explores three directions of Saber:

1. The stack usage for the NTT approach.
2. The compatibility of masking, a technique for protecting from side-channel attacks, with NTTs.
3. The best approach for multiplying polynomials resisting timing attacks on Cortex-M3.

New records were set in all three directions. In another paper, “Neon NTT: Faster Dilithium, Kyber, and Saber on Cortex-A72 and Apple M1,” the focus turns to the Armv8-A architecture for Dilithium, Kyber, and Saber. A new implementation idea, “Barrett multiplication” for modular multiplication with Armv8-A and “asymmetric multiplication” for the matrix-to-vector multiplication, was introduced. The new implementation is 1.7-2.1 times faster on Cortex-A72 and Apple M1 compared to the previous work.  Because this is open source software, these ideas and programs should find wide application, especially Barrett Multiplication. 

Other Works on Non-lattice-based Submissions

Academia Sinica is also involved in the papers “Rainbow on Cortex-M4,” “Optimizing BIKE for the Intel Haswell and ARM Cortex-M4,” and “Classic McEliece on the ARM Cortex-M4.”  Vast speed-up compared to previous works and state of the art methods was achieved.